Лекция N 32

Нелинейные магнитные цепи при постоянных потоках.
Основные понятия и законы магнитных цепей

При решении электротехнических задач все вещества в магнитном отношении делятся на две группы:

Для концентрации магнитного поля и придания ему желаемой конфигурации отдельные части электротехнических устройств выполняются из ферромагнитных материалов. Эти части называют магнитопроводами или сердечниками. Магнитный поток создается токами, протекающими по обмоткам электротехнических устройств, реже – постоянными магнитами. Совокупность устройств, содержащих ферромагнитные тела и образующих замкнутую цепь, вдоль которой замыкаются линии магнитной индукции, называют магнитной цепью.

Магнитное поле характеризуется тремя векторными величинами, которые приведены в табл. 1.

 

Таблица 1. Векторные величины, характеризующие магнитное поле

Наименование

Обозначение

Единицы

измерения

Определение

Вектор магнитной индукции

Тл

(тесла)

Векторная величина, характеризующая силовое действие магнитного поля на ток по закону Ампера

Вектор намагниченности

А/м

Магнитный момент единицы объема вещества

Вектор напряженности магнитного поля

А/м

,

где Гн/м- магнитная постоянная

 

Основные скалярные величины, используемые при расчете магнитных цепей, приведены в табл. 2.

Таблица 2. Основные скалярные величины, характеризующие магнитную цепь

Наименование

Обозначение

Единица

измерения

Определение

Магнитный поток

Вб

(вебер)

Поток вектора магнитной индукции через поперечное сечениемагнитопровода

Магнитодвижущая (намагничивающая) сила МДС (НС)

A

где -ток в обмотке,-число витков обмотки

Магнитное напряжение

А

Линейный интеграл от напряженности магнитного поля , где и -граничные точки участка магнитной цепи, для которого определяется

 

Характеристики ферромагнитных материалов

Свойства ферромагнитных материалов характеризуются зависимостью магнитной индукции от напряженности магнитного поля. При этом различают кривые намагничивания, представляющие собой однозначные зависимости , и гистерезисные петли - неоднозначные зависимости  (см. рис. 1).

 

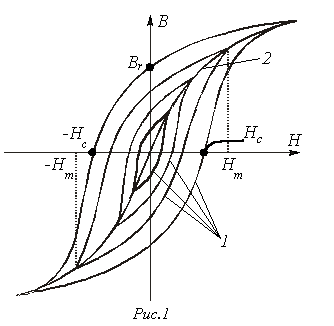
Основные понятия, характеризующие зависимости , приведены в табл. 3.

 

Таблица 3. Основные понятия, характеризующие зависимости  

Понятие

Определение

Магнитный  гистерезис

Явление отставания изменения магнитной индукции B от изменения напряженности магнитного поля H

Статическая петля гистерезиса

Зависимость ,получаемая путем ряда повторных достаточно медленных изменений магнитной напряженности в пределах выбранного значения(см. кривые 1 на рис. 1).

Площадь статической петли гистерезиса характеризует собой потери на магнитный гистерезис за один период изменения магнитной напряженности

Начальная кривая намагничивания

Кривая намагничивания предварительно размагниченного ферромагнетика (B=0;H=0) при плавном изменении магнитной напряженности H. Представляет собой однозначную зависимостьи обычно близка к основной кривой намагничивания

Основная кривая намагничивания

Геометрическое место вершин петель магнитного гистерезиса (см. кривую 2 на рис. 1). Представляет собой однозначную зависимость

Предельная петля гистерезиса (предельный цикл)

Симметричная петля гистерезиса при максимально возможном насыщении

Коэрцитивная (задерживающая) сила

Напряженность магнитного поля Нс, необходимая для доведения магнитной индукции в предварительно намагниченном ферромагнетике до нуля. В справочной литературе обычно дается для предельной петли гистерезиса

Остаточная индукция

Значение индукции магнитного поля Вr  при равной нулю напряженности магнитного поля. В справочной литературе обычно дается для предельного цикла

 

Магнитомягкие и магнитотвердые материалы

Перемагничивание ферромагнитного материала связано с расходом энергии на этот процесс. Как уже указывалось, площадь петли гистерезиса характеризует энергию, выделяемую в единице объема ферромагнетика за один цикл перемагничивания. В зависимости от величины этих потерь и соответственно формы петли гистерезиса ферромагнитные материалы подразделяются на магнитомягкие и магнитотвердые. Первые характеризуются относительно узкой петлей гистерезиса и круто поднимающейся основной кривой намагничивания; вторые обладают большой площадью гистерезисной петли и полого поднимающейся основной кривой намагничивания.

             Магнитомягкие материалы (электротехнические стали, железоникелевые сплавы, ферриты) определяют малые потери в сердечнике и применяются в устройствах, предназначенных для работы при переменных магнитных потоках (трансформаторы, электродвигатели и др.). Магнитотвердые материалы (углеродистые стали, вольфрамовые сплавы и др.) используются для изготовления постоянных магнитов.

 

Статическая и дифференциальная магнитные проницаемости

Статическая магнитная проницаемость (в справочниках  начальная  и максимальная)

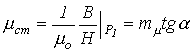(1)

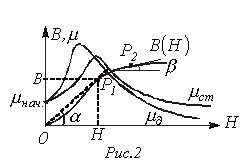
определяется по основной кривой намагничивания и в силу ее нелинейности не постоянна по величине (см.   рис. 2).

Величина  определяется тангенсом угла наклона касательной в начале кривой .

Кроме статической вводится понятие дифференциальной магнитной проницаемости, устанавлива-ющей связь между бесконечно малыми приращениями индукции и напряженности


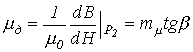.      (2)

 

Кривые  и  имеют две общие точки: начальную и точку, соответствующую максимуму  (см. рис. 2).

При учете петли гистерезиса статическая магнитная проницаемость, определяемая согласно (1), теряет смысл. При этом значения  определяют по восходящей ветви петли при  и по нисходящей – при .

При переменном магнитном потоке вводится также понятие динамической магнитной проницаемости, определяемой соотношением, аналогичным (2), по динамической характеристике.

 

Основные законы магнитных цепей

В основе расчета магнитных цепей лежат два закона (см. табл. 4).

 

Таблица 4.. Основные законы магнитной цепи

Наименование
закона

Аналитическое выражение закона

Формулировка закона

Закон (принцип) непрерывности магнитного потока

Поток вектора магнитной индукции через замкнутую поверхность равен нулю

Закон полного тока

Циркуляция вектора напряженности вдоль произвольного контура равна алгебраической сумме токов, охватываемых этим контуром

При анализе магнитных цепей и, в первую очередь, при их синтезе обычно используют следующие допущения:

- магнитная напряженность, соответственно магнитная индукция, во всех точках поперечного сечения магнитопровода одинакова

- потоки рассеяния отсутствуют (магнитный поток через любое сечение неразветвленной  части магнитопровода одинаков);

- сечение воздушного зазора равно сечению прилегающих участков магнитопровода.

Это позволяет использовать при расчетах законы Кирхгофа и  Ома для магнитных цепей (см. табл. 5), вытекающие из законов, сформулированных в табл. 4.

 

Таблица 5. Законы Кирхгофа и Ома для магнитных цепей

Наименование закона

Аналитическое выражение  закона

Формулировка закона

Первый закон   Кирхгофа

Алгебраическая сумма магнитных потоков в узле магнитопровода равна нулю

Второй закон Кирхгофа

Алгебраическая сумма падений магнитного напряжения вдоль замкнутого контура равна алгебраической сумме МДС, действующих в контуре

Закон Ома

где

Падение магнитного напряжения на участке магнитопровода длиной  равно произведению магнитного потока и магнитного сопротивления  участка

Сформулированные законы и понятия магнитных цепей позволяют провести формальную аналогию между основными величинами и законами, соответствующими электрическим и магнитным цепям, которую иллюстрирует табл. 6.

 

Таблица 6. Аналогия величин и законов для электрических и магнитных цепей

Электрическая цепь

Магнитная цепь

Ток

Поток

ЭДС

МДС (НС)

Электрическое сопротивление

Магнитное сопротивление

Электрическое напряжение

Магнитное напряжение

Первый закон Кирхгофа:

Первый закон Кирхгофа:

Второй закон Кирхгофа:

Второй закон Кирхгофа:

Закон Ома:

Закон Ома:

 

Литература

  1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
  2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
  3. Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.

Контрольные вопросы и задачи

  1. Какие векторные величины характеризуют магнитное поле?
  2. Какие основные понятия связаны с петлей гистерезиса?
  3. Что характеризует площадь гистерезисной петли?
  4. Какие ферромагнитные материалы и почему используются для изготовления сердечников для машин переменного тока?
  5. Назовите основные законы магнитного поля?
  6. В чем заключаются основные допущения, принимаемые при расчете магнитных цепей?
  7. Проведите аналогию между электрическими и магнитными цепями?
  8. Магнитная индукция в сердечнике при напряженности Н=200 А/м составляет В=1,0 Тл. Определить относительную магнитную проницаемость.

    9. Ответ: .

  9. Определить магнитное сопротивление участка цепи длиной  и сечением , если .

    10. Ответ: .

  10. В условиях предыдущей задачи определить падение магнитного напряжения на участке, если индукция В=0,8 Тл.

    11. Ответ: .